信号采样

采样器： 把连续信号变换为脉冲序列
采样器的采样过程可以使用一个周期性闭合的采样开关 S 表示

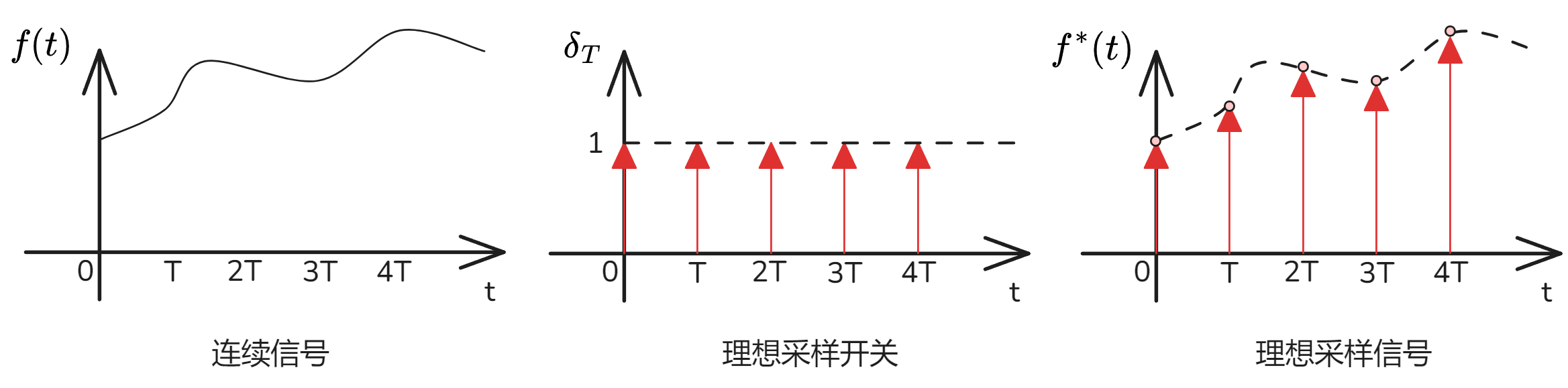
理想单位脉冲序列（理想采样开关）：

\begin{aligned} δ_{T} (t) & = \sum_{n = 0}^{\infty} δ (t - n T) \end{aligned}

$δ (t - n T)$ 是出现在时刻 $t = n T$ 强度为 1 的单位脉冲
连续信号在采样的瞬时点 $t = n T$ 为： $e (n T)$
则采样信号表示为：

\begin{array}{r} e^{*} (t) = e (t) δ_{T} (t) = \sum_{n = 0}^{\infty} e (n T) δ_{T} (t - n T) \end{array}

\begin{aligned} E^{*} (s) & = L [e^{*} (t)] \\ = L [\sum_{n = 0}^{\infty} e (n T) δ_{T} (t - n T)] \\ = \sum_{n = 0}^{\infty} e (n T) L [δ_{T} (t - n T)] \\ = \sum_{n = 0}^{\infty} e (n T) e^{- n T s} \end{aligned}

\begin{aligned} e^{*} (t) & = \frac{1}{T} \sum_{n = - \infty}^{\infty} e (t) e^{j n ω_{s} t} \\ E^{*} (s) & = \frac{1}{T} \sum_{n = - \infty}^{\infty} E (s + j n ω_{s}) \\ E^{*} (j ω) & = \frac{1}{T} \sum_{n = - \infty}^{\infty} E [j (ω + n ω_{s})] \end{aligned}

如果采样器的输入信号具有有限带宽，并且有直到 $ω_{h}$ 的频率分量（即最高频率为 $ω_{h}$ ）
则使得信号完全从采样信号中恢复过来的采样周期 $T$ 满足：(采样频率 $ω_{s} \geq 2 ω_{h}$ )

\begin{aligned} ω_{s} \geq 2 ω_{h} \Rightarrow T = \frac{2 π}{ω_{s}} & \leq \frac{2 π}{2 ω_{h}} \end{aligned}

工程实践中，一般不取等号

采样周期小于最小时间常数的一半，例子：

\begin{array}{r} \frac{1}{(s + 1) (s + 2)} T_{1} = 1, T_{2} = \frac{1}{2} T < \frac{1}{4} \end{array}

简单理解：就是找频率最高的分量（即最小的时间常数），采样频率大于两倍的最高频率，所以采样周期就小于最小的时间常数的一半